ローレンツ曲線とは
都道府県別の年間雷日数ランキングから度数分布表を作成する。
| 階級 | 度数 | 相対度数 | 累積相対度数 (都道府県) | 各階級の雷日数合計 | 相対同数 (雷日数) | 累積相対同数 (雷日数) |
| 0以上10未満 | 2 | 0.042553191 | 0.042553191 | 18.1 | 0.021221714 | 0.021221714 |
| 10以上20未満 | 26 | 0.553191489 | 0.595744681 | 394.4 | 0.462422324 | 0.483644038 |
| 20以上30未満 | 14 | 0.29787234 | 0.893617021 | 264.6 | 0.310235667 | 0.793879705 |
| 30以上40未満 | 4 | 0.085106383 | 0.978723404 | 133.4 | 0.156407551 | 0.950287255 |
| 40以上50未満 | 1 | 0.021276596 | 1 | 42.4 | 0.049712745 | 1 |
| 合計 | 47 | 1 | 852.9 | 1 |
年間雷日数が0日以上30日未満の都道府県は全国で90%を占めています。
つまり残りの10%の都道府県が年間雷日数が30日以上あることになります。
都道府県ごとの年間雷日数の分布は偏っているように見えます。
この偏り=不均等さを表すローレンツ曲線といいます。
ローレンツ曲線は2つの累積相対度数から作成されます。
ローレンツ曲線はどういったときに使う?
ローレンツ曲線は、経済学や社会学などの分野で所得や富の不均等な分布を可視化するために使われます。具体的には以下のようなばあに使用されます。
- 所得格差の可視化:ある地域や国の住民の所得格差を表すことができます。縦軸に累積所得比率、横軸に累積人口比率をプロットすることで、どの程度の人々がどの程度の所得を得ているかがわかります。
- 貧困層の割合の把握:ある地域や国の貧困層の割合を把握することができます。例えば上位20%の人々が全体の80%の所得を持っている場合、下位20%の人々がどの程度の所得しか持っていないかがわかります。
- 所得格差の推移の追跡:時間経過に伴う所得格差の変化を追跡することができます。これにより、ある政策や社会的な変化が所得格差に与える影響を評価することができます。
ローレンツ曲線 グラフ
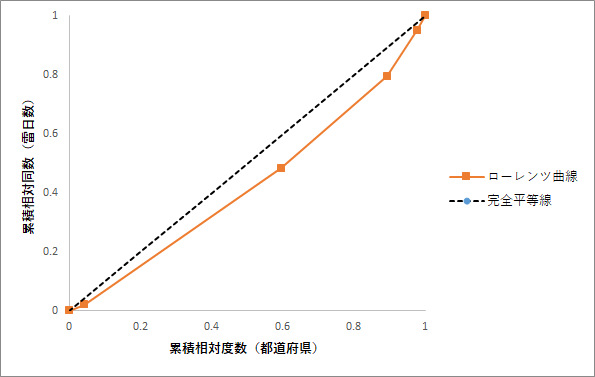
言うほど偏りないな。。データの例が悪いな
ジニ係数とは
度数分布表やローレンツ曲線を作成することで、偏りや不均等さが確認できます。
それらを数値で表したものがジニ係数です。
求め方はローレンツ曲線と完全平等戦の間の面積(オレンジ部分)を2倍した値になります。
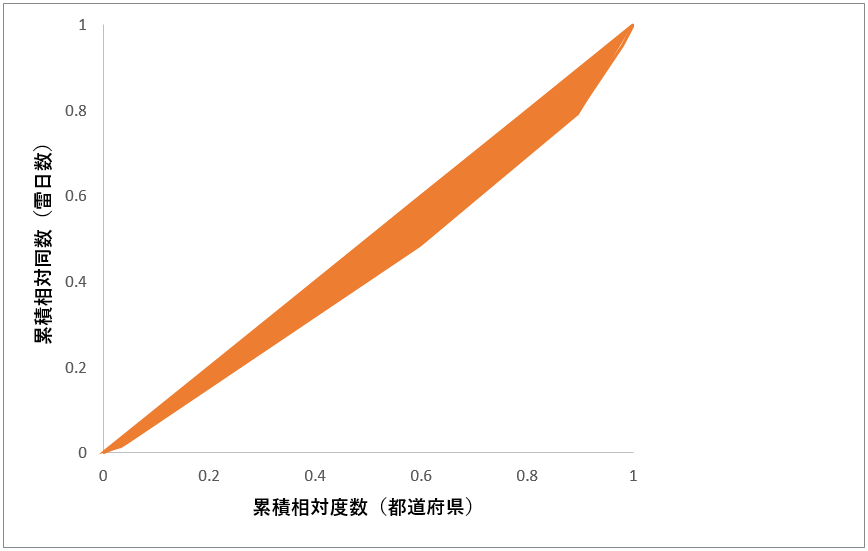
ジニ係数を算出する
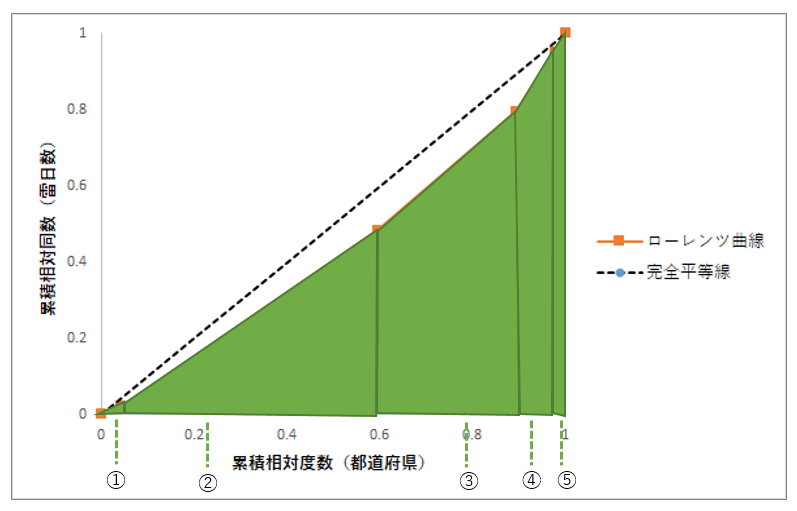
ジニ係数を求めるためには下記情報が必要
(A)「完全平等線とx軸(横軸)とで囲まれた部分の面積」
(B)「①~⑤の三角形または台形の面積の合計」
ジニ係数は下記計算式から求められる
ジニ係数 = ((A) ー (B)) × 2
(A)「完全平等線とx軸(横軸)とで囲まれた部分の面積」= 1 * 1 * 0.5 = 0.5
(B)「①~⑤の三角形または台形の面積の合計」は下記
| 種類 | 計算式 | |
| ① | 三角形 | 0.04255319149 * 0.02122171415 * 0.5 = 0.000451525832985496 |
| ② | 台形 | (0.02122171415 + 0.483644038) * (0.5957446809 – 0.04255319149) * 0.5 = 0.139643718691979 |
| ③ | 台形 | (0.483644038 + 0.7938797045) * (0.8936170213 – 0.5957446809) * 0.5 = 0.190269493547521 |
| ④ | 台形 | (0.7938797045 + 0.9502872552) * (0.9787234043 – 0.8936170213) * 0.5 = 0.0742198706440869 |
| ⑤ | 台形 | (0.9502872552 + 1) * (1 – 0.9787234043) * 0.5 = 0.0207477367138765 |
| 面積合計 | 0.425332345430449 |
ジニ係数 = ((A) ー (B)) × 2
= (0.5 – 0.425332345430449) * 2
= 0.149335309139102


コメント